|
Электротехника
| |
| SlaVe4U | Дата: Среда, 12.01.2011, 02:39 | Сообщение # 1 |
|
Главный Администратор
Группа: Администраторы
Сообщений: 320
Награды: 23
Репутация: 222
Статус: Offline
| 1. Алгебра Буля. Основные законы алгебры Буля.
АЛГЕБРА БУЛЯ
- исторически первый раздел математической логики, разработанный ирландским логиком и математиком Дж. Булем в середине XIX в. Буль применил алгебраические методы для решения логических задач и сформулировал на языке алгебры некоторые фундаментальные законы мышления. Буль представляет логику как алгебру классов (будем обозначать их символами А, В, С,...). Основными операциями в А. Б. являются: сложение классов AA.B; умножение классов ААВ; дополнение класса А&. Свойства этих операций описываются следующими аксиомами: la. Al(B©=(ACB) BC - ассоциативность сложения;
16. A1(B©= (ACВ) ВC - ассоциативность умножения;
2a.A2B= BBA - коммуникативность сложения;
2б.А2В =ВВА - коммуникативность умножения;
3a.A3(В(С)= =(AСB) B(A© - дистрибутивность сложения относительно умножения;
36.A3(B©==(ACB) B(A© - дистрибутивность умножения относительно сложения.
В А. Б. существуют два элемента 0 и 1, операции с которыми
подчиняются следующим соотношениям: AA0=A;
AA1=A;
AAA&=1;
AAA&=0. Характерная особенность А.Б. заключается в том, что в ней отсутствуют коэффициенты и показатели степеней. Сумма двух А равна А: А А=А, а не 2А, как в обычной алгебре. Точно так же и произведение двух A равно A: ААА=А, а не A2.
Важным законом А. Б. является принцип двойственности, согласно которому если в некотором справедливом равенстве мы заменим все вхождения й на и на , 1 на 0 и 0 на 1, то получим равенство, двойственное первому и также справедливое. Примерами двойственных равенств являются приведенные выше аксиомы.
А.Б. широко применяется при проектировании и проверке электрических схем, в которых используются реле, работающие по принципу "да - нет", при программировании и проектировании ЭВМ, в операциях с переключателями, сигналами, схемами. В современной математической логике этот раздел значительно усовершенствован и разрабатывается как теория булевых алгебр, в том числе как алгебра множеств, алгебра высказываний и т. п. В области традиционной логики соотношения А. Б. часто используются для иллюстрации и прояснения отношений между объемами понятий. Основные законы алгебры Буля
1.2.Основные законы алгебры Буля.
1. Комплементарность.
a*a'=0; a+a'=1
2. Идемпотентный закон.
а*а=а; а+а=а
3. Переместительный закон.
а+в=в+а; ав=ва
4. Сочетательный закон.
(а+в)+с=а+(в+с); (ав)*с=а*(вс)
5. Закон поглощения.
а+ав=а(1+в)=а; а(а+в)=а+ав=а
6. Распределительный закон.
а(в+с)=ав+ас; (а+в)(а+с)=а+вс
/* (а+в)(а+с)=а*а+ав+ас+вс=(а+ав+ас)+вс=
=а(1+в+с)+вс=а+вс */
7. Закон склеивания
ав+ав'=а(в+в')=а;
(а+в)(а+в')=а+ав+ав'+вв'=а+а(в+в)+0=
=а+а*1=а+а=а
8.Правила де Mоргана.
____ ____
_ _ _ _
а+в = а*в; а*в = а*в
_________ __________
_ _ _ _ _ _
/*а+в+...+z = а*в...*z; а*в*...*z = а+в+...+z */ Заучивать все логические законы и запоминать их названия нет ни-
какого смысла,тем более,что на практике используются 2-3 из них(законы
поглощения и склеивания,правила Де Моргана).Значительно важнее осмыс-
лить эти законы и научиться применять.
С помощью правил де Моргана легко реализуются логические схемы на
базе интегральных схем(ИС) так называемого функционально полного бази-
са(ФПБ).ФПБ характерен тем,что на его основе можно построить любую
сколь угодно сложную схему,в том числе и самую сложную вычислительную
машину без применения других ИС.К ФПБ относятся ИС типа И-НЕ,а также
ИЛИ-НЕ.Таким образом,на очень простом элементе типа И-НЕ может быть
построена,например,сложная система управления ракетой.Только в этой
системе управления простые элементы И-НЕ сгруппированы в большие ин-
тегральне схемы(БИС),которые выполняют функции процессора,памяти и то-
му подобных сложных устройств.
Пусть нам необходимо построить схему,реализующую функцию
y = x1x2 + x3x4.Используя формулу де Моргана,получим следующее соотно-
шение:
y = x1x2 + x3x4 = ((x1x2)'(x3x4)')'.
Таким образом,мы выразили исходную функцию с помощью одних только
элементов И-НЕ.Схема реализации заданной функции представлена на ри-
сунке. ------¬
X1--+ & ¦ (x1x2)'
Х2--+ о-------¬ ------¬
L------ L-------+ & ¦ y=((x1x2)'(x3x4)')'=x1x2+x3x4
--------+ о--
------¬ ¦ L------
X3--+ & ¦ ¦
Х4--+ о--------
L------ (x3x4)'

|
| |
| |
| SlaVe4U | Дата: Среда, 12.01.2011, 02:40 | Сообщение # 2 |
|
Главный Администратор
Группа: Администраторы
Сообщений: 320
Награды: 23
Репутация: 222
Статус: Offline
| 2. Булевы функции двух переменных. Условные графические обозначения логических элементов, реализующих эти функции.
Бу́лева фу́нкция (или логи́ческая функция, или функция а́лгебры ло́гики) от n переменных — в дискретной математике отображение Bn → B, где B = {0,1} — булево множество. Элементы булева множества 1 и 0 обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определенного смысла. Неотрицательное целое число n называют арностью или местностью функции, в случае n = 0 булева функция превращается в булеву константу. Элементы декартова произведения Bn называют булевыми векторами. Множество всех булевых функций от любого числа переменных часто обозначается P2, а от n переменных — P2(n). Булевы функции названы так по фамилии математика Джорджа Буля.
Основные сведения Каждая булева функция арности n полностью определяется заданием своих значений на своей области определения, то есть на всех булевых векторах длины n. Число таких векторов равно 2n. Поскольку на каждом векторе булева функция может принимать значение либо 0, либо 1, то количество всех n-арных булевых функций равно 22n. Поэтому в этом разделе рассматриваются только простейшие и важнейшие булевы функции. То, что каждая булева функция задаётся конечным массивом данных, позволяет представлять их в виде таблиц. Такие таблицы носят название таблиц истинности и в общем случае имеют вид:x1 x2 … xn f(x1,x2,…,xn)
0 0 … 0 f(0,0,…,0)
1 0 … 0 f(1,0,…,0)
0 1 … 0 f(0,1,…,0)
1 1 … 0 f(1,1,…,0)
0 1 … 1 f(0,1,…,1)
1 1 … 1 f(1,1,…,1) Практически все булевы функции малых арностей (0, 1, 2 и 3) сложились исторически и имеют конкретные имена. Если значение функции не зависит от одной из переменных (то есть строго говоря для любых двух булевых векторов, отличающихся лишь в значении этой переменной, значение функции на них совпадает), то эта переменная называется фиктивной.
Нульарные функции При n = 0 количество булевых функций сводится к двум 220 = 21 = 2, первая из них тождественно равна 0, а вторая 1. Их называют булевыми константами — тождественный нуль и тождественная единица.
[править]
Унарные функции При n = 1 число булевых функций равно 221 = 22 = 4. Определение этих функций содержится в следующей таблице. Таблица значений булевых функций от одной переменной:x 0 x̅ x 1
0 0 1 0 1
1 0 0 1 1 Названия булевых функций от одной переменной:Обозначение Название
0 тождественный ноль, тождественная ложь, тождественное "НЕТ"
x̅, ¬x, x' отрицание, логическое "НЕТ", "НЕ", "НИ", "NOT"(англ.), "NO"(англ.)
x тождественная функция, логическое "ДА", "YES"(англ.)
1 тождественная единица, тождественная истина, тождественное "ДА", тавтология [править]
Бинарные функции При n = 2 число булевых функций равно 22² = 24 = 16.

|
| |
| |
| SlaVe4U | Дата: Среда, 12.01.2011, 02:40 | Сообщение # 3 |
|
Главный Администратор
Группа: Администраторы
Сообщений: 320
Награды: 23
Репутация: 222
Статус: Offline
| Таблица значений булевых функций от двух переменных:x y 0 x↓y x←y x x→y y x⊕y x|y x & y x ≡ y y x→y x x←y x ∨ y 1
0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
0 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
1 0 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 Названия булевых функций от двух переменных:Обозначение Название
0 тождественный ноль, тождественная ложь, тождественное "НЕТ"
x ↓ y, x ИЛИ-НЕ y, ИЛИ-НЕ(x,y), x NOR y, NOR(x,y) НЕ- 2ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, функция Да́ггера, функция Ве́бба, стрелка Пи́рса
x < y, x ← y, x LT y, LT(x,y) меньше, инверсия обратной импликации
x, НЕ1(x,y), NOT1(x,y), x', ¬x отрицание (негация, инверсия) первого операнда
x > y, x → y, x GT y, GT(x,y) больше, инверсия прямой импликации
y, НЕ2(x,y), NOT2(x,y), y', ¬y отрицание (негация, инверсия) второго операнда
x ⊕ y, x +2 y, x ≠ y, x >< y, x <> y, x XOR y, XOR(x,y) сложение по модулю 2, не равно, измена, исключающее «или»
x | y, x NAND y, NAND(x,y), x И-НЕ y, И-НЕ(x,y) НЕ-2И, 2И-НЕ, антиконъюнкция, штрих Ше́ффера
x & y, x • y, xy, x ∧ y, x AND y, AND(x,y), x И y, И(x,y), min(x,y) 2И, конъюнкция
x ≡ y, x = y, x EQV y, EQV(x,y), x ~ y, x ↔ y равенство, эквивалентность
y, ДА2(x,y), YES2(x,y) второй операнд
x → y, x ≤ y, x ⊃ y, x LE y, LE(x,y) меньше или равно, прямая (материальная) импликация (от первого аргумента ко второму)
x, ДА1(x,y), YES1(x,y) первый операнд
x ← y, x ≥ y, x ⊂ y, x GE y, GE(x,y) больше или равно, обратная импликация (от второго аргумента к первому)
x ∨ y, x + y, x ИЛИ y, ИЛИ(x,y), x OR y, OR(x,y), max(x,y) 2ИЛИ, дизъюнкция
1 тождественная единица, тождественная истина, тождественное "ДА", тавтология

|
| |
| |
| SlaVe4U | Дата: Среда, 12.01.2011, 02:41 | Сообщение # 4 |
|
Главный Администратор
Группа: Администраторы
Сообщений: 320
Награды: 23
Репутация: 222
Статус: Offline
| 3. Комбинационные логические цепи и их минимизация при помощи карты Карно.
Комбинационные логические цепи Основные положения алгебры логики Анализ и синтез логических схем осуществляется на базе аппарата алгебры логики или булевой алгебры [9]. Излагать весь аппарат не имеет смысла, так как в инженерной практике используются два-три закона алгебры логики. В алгебре логики переменные могут принимать только два значения, 0 или 1. Для двух аргументов существуют 16 логических функций (операций, логических действий). Над переменными в основном производятся три логических действия: сложение, умножение, отрицание (инверсия), что соответствует функциям ИЛИ, И, НЕ. Все функции в булевой алгебре могут быть описаны с помощью таблицы истинности. В нижеследующих таблицах описаны функции И(f1), ИЛИ(f2),НЕ(f3).
Аргументы Функции
x2 x1 f1 f2
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 1 Аргумент Функция
x f3
0 1
1 0
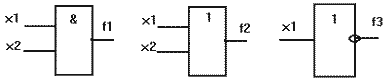
Вместо функции И часто используется термин "конъюнкция", вместо функции ИЛИ - термин "дизъюнкция". По ЕСКД логические элементы, реализующие функции И(f1), ИЛИ(f2), НЕ(f3), изображаются так, как представлено на рисунке. При написании логических формул для функции И используются следующие знаки : &, U, точка или ее отсутствие; для функции ИЛИ +,^. Функция НЕ обозначается штрихом над аргументом. Мы для обозначения отрицания будем использовать апостроф. Таким образом, можно записать:
f1 = x2&x1 = x2^x1 = x2x1
f2 = x2Ux1 = x2+x1
f3 = x'

|
| |
| |
| SlaVe4U | Дата: Среда, 12.01.2011, 02:42 | Сообщение # 5 |
|
Главный Администратор
Группа: Администраторы
Сообщений: 320
Награды: 23
Репутация: 222
Статус: Offline
| Основные законы алгебры Буля Как уже отмечалось, в булевой алгебре все операции осуществляются с логическими переменными и подчиняются законам алгебры логики. Опишем некоторые из них.
а) Переместительный закон
а + в = в + а; ав = ва
б) Сочетательный закон
(а + в) + с = а + (в + с); (ав)с = а(вс)
в) Распределительный закон
а(в + с) = ав + ас; а + вс = (а + в)(а + с)
г) Закон поглощения
а + ав = а(1 + в) = а; а(a + в) = а + ав = а
д) Закон склеивания
ав + ав' = а; (а + в)(а + в') = а
е) Идемпотентный закон
a + a = a; a & a = a
ё) Правила де Моргана
Эти правила справедливы для любого числа аргументов.
а + в + с + .... + z = ( а'в'с'...z' )'
авс... = ( а' + в' + с' + ... + z' )' Эти правила можно описать таким алгоритмом. Для перехода от логической суммы к логическому произведению необходимо проделать следующие операции :
проинвертировать все слагаемые в отдельности;
заменить знаки дизъюнкции на знаки конъюнкции;
проинвертировать получившееся выражение. Аналогично выполняется переход от логического произведения к логической сумме.В инженерной практике используются лишь правила де Моргана и закон склеивания(в виде карт Карно). Кроме основных функций И, ИЛИ, НЕ в алгебре логики часто используются функции равнозначности (эквивалентности) и неравнозначности (сумма по модулю 2 ). Для обозначения этих функций используются следующие знаки : равнозначность - ~ , сумма по модулю 2 - . Содержание этих функций отражено в таблице .
a b f4 f5
0 0 1 0
0 1 0 1
1 0 0 1
1 1 1 0 Из таблицы получаем:
f4 = а ~ в = а'в' + ав
f5 = a в = а'в + ав'
Из таблицы видно, что
f4 = f5' или f5 = f4'
Таким образом,
а'в' + ав = ( ав' + а'в )' , или
а~в = ( а в )' , а в = (а~в)'
1.3. Синтез комбинационных схем Синтез комбинационных схем можно проиллюстрировать решением простой задачи. Задача 1 Приёмная комиссия в составе трех членов комиссии и одного председателя решает судьбу абитуриента большинством голосов. В случае равного распределения голосов большинство определяется той группой, в которой оказался председатель приемной комиссии. Построить автомат, обеспечивающий определение большинства голосов. Решение Пусть f - функция большинства голосов. f = 1, если большинство членов комиссии проголосовало за приём абитуриента, и f = 0 в противном случае. Обозначим через x4 голос председателя комиссии. x4 = 1, если председатель комиссии проголосовал за приём абитуриента. x3, x2, x1 - голоса членов приёмной комиссии. С учётом вышеуказанных допущений условие задачи можно однозначно представить в виде таблицы истинности. Заполнение таблицы осуществляем с учётом того, что функция f является полностью определённой, т.е. она определена на всех возможных наборах переменных x1 - x4. Для n входных переменных существует N = 2n наборов переменных. В нашем примере N = 24 = 16 наборов. Записывать эти наборы можно в любом порядке, но лучше в порядке возрастания двоичного кода.
x4 x3 x2 x1 f
0 0 0 0 0
0 0 0 1 0
0 0 1 0 0
0 0 1 1 0
0 1 0 0 0
0 1 0 1 0
0 1 1 0 0
0 1 1 1 1
1 0 0 0 0
1 0 0 1 1
1 0 1 0 1
1 0 1 1 1
1 1 0 0 1
1 1 0 1 1
1 1 1 0 1
1 1 1 1 1
1.4. Минимизация полностью определённых булевых функций. Существует несколько способов минимизации булевых функций. Прежде всего это метод Квайна-Мак-Класки, метод Блека-Порецкого и метод минимизации с помощью карт Карно или диаграмм Вейча [13, 22, 29]. Здесь будет подробно излагаться метод карт Карно, как самый удобный метод, позволяющий быстро решать задачи минимизации булевых функций от достаточно большого числа аргументов (6-12). При этом получается минимальная форма в базисе И, ИЛИ, НЕ. Существуют карты Карно на 2 , 3 , 4 , 5 и 6 переменных[13,22]. Причем последние стали использоваться достаточно недавно. На рисунке представлены карты Карно для 2, 3, 4, 5 и 6 аргументов.

|
| |
| |
| SlaVe4U | Дата: Среда, 12.01.2011, 02:42 | Сообщение # 6 |
|
Главный Администратор
Группа: Администраторы
Сообщений: 320
Награды: 23
Репутация: 222
Статус: Offline
| Карты и прямоугольники Карно. Метод Карно основан на законе склеивания. Склеиваются наборы , отличающиеся друг от друга значением одного разряда. Такие наборы называются соседними. Карно закодировал клетки своей карты так ,что в соседних клетках оказались соседние, а значит, склеивающиеся наборы. Соседними могут быть не только отдельные клетки, которые мы назовем элементарными квадратами Карно, но и целые группы соседних клеток(назовем их прямоугольниками Карно). Под прямоугольником Карно[13] будем понимать некоторую, зачастую разрозненную фигуру покрытия, все соседние клетки которой закодированы соседними наборами. Например, на вышеприведённом рисунке в поле карты для 4-х переменных изображён прямоугольник Карно P, состоящий из четырёх элементарных квадратов Карно, описываемых наборами x4'x3'x2'x1' , x4'x3'x2x1' , x4x3'x2'x1' , x4x3'x2x1' . Если над логической суммой этих четырёх наборов произвести последовательно операции склеивания, то мы аналитически получим результат в виде импликанты (под импликантой будем понимать неполный набор)x3'x1'. Карта Карно позволяет получить этот результат графически значительно быстрее и проще. Для решения этой задачи используем алгоритм графической минимизации.Кстати говоря,сам Карно никакого алгоритма не предложил.

|
| |
| |
| SlaVe4U | Дата: Среда, 12.01.2011, 02:45 | Сообщение # 7 |
|
Главный Администратор
Группа: Администраторы
Сообщений: 320
Награды: 23
Репутация: 222
Статус: Offline
| 4. Дешифраторы. Минимизация двоично-десятичных дешифраторов.
У этого термина существуют и другие значения, см. Дешифратор (значения).
Пример дешифратора 2×4
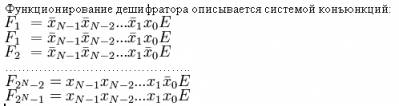
Дешифратор (декодер) — комбинационное устройство, преобразующее n-разрядный двоичный, троичный или k-ичный код в -ичный одноединичный код, где - основание системы счисления. Логический сигнал появляется на том выходе, порядковый номер которого соответствует двоичному, троичному или k-ичному коду.
Дешифраторы являются устройствами, выполняющими двоичные, троичные или k-ичные логические функции (операции). Двоичный дешифратор работает по следующему принципу: пусть дешифратор имеет N входов, на них подано двоичное слово xN − 1xN − 2...x0, тогда на выходе будем иметь такой код, разрядности меньшей или равной 2N, что разряд, номер которого равен входному слову, принимает значение единицы, все остальные разряды равны нулю. Очевидно, что максимально возможная разрядность выходного слова равна 2N. Такой дешифратор называется полным. Если часть входных наборов не используется, то число выходов меньше 2N, и дешифратор является неполным. Часто дешифраторы дополняются входом разрешения работы E. Если на этот вход поступает единица, то дешифратор функционирует, в ином случае на выходе дешифратора вырабатывается логический ноль вне зависимости от входных сигналов. Существуют дешифраторы с инверсными выходами, у такого дешифратора выбранный разряд показан нулём. Функционирование дешифратора описывается системой конъюнкций:
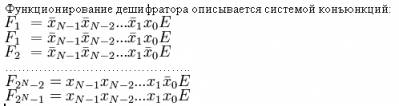
Обратное преобразование осуществляет шифратор. Дешифраторы. Это комбинационные схемы с несколькими входами и выходами, преобразующие код, подаваемый на входы в сигнал на одном из выходов. На выходе дешифратора появляется логическая единица, на остальных — логические нули, когда на входных шинах устанавливается двоичный код определённого числа или символа, то есть дешифратор расшифровывает число в двоичном, троичном или k-ичном коде, представляя его логической единицей на определённом выходе. Число входов дешифратора равно количеству разрядов поступающих двоичных, троичных или k-ичных чисел. Число выходов равно полному количеству различных двоичных, троичных или k-ичных чисел этой разрядности. Для n-разрядов на входе, на выходе 2n, 3n или kn. Чтобы вычислить, является ли поступившее на вход двоичное, троичное или k-ичное число известным ожидаемым, инвертируются пути в определённых разрядах этого числа. Затем выполняется конъюнкция всех разрядов преобразованного таким образом числа. Если результатом конъюнкции является логическая единица, значит на вход поступило известное ожидаемое число. Из логических элементов являющихся дешифраторами можно строить дешифраторы на большое число входов. Каскадное подключение таких схем позволит наращивать число дифференцируемых переменных.

|
| |
| |
| SlaVe4U | Дата: Среда, 12.01.2011, 02:47 | Сообщение # 8 |
|
Главный Администратор
Группа: Администраторы
Сообщений: 320
Награды: 23
Репутация: 222
Статус: Offline
| 5, 6. Транзисторно- транзисторная логика. Особенности построения и применения. Основные параметры. Типовой логический элемент.
Транзисторно-транзисторная логика (ТТЛ, TTL) — разновидность цифровых логических микросхем, построенных на основе биполярных транзисторов и резисторов. Название транзисторно-транзисторный возникло из-за того, что транзисторы используются как для выполнения логических функций (например, И, ИЛИ), так и для усиления выходного сигнала (в отличие от резисторно-транзисторной и диодно-транзисторной логики). Простейший базовый элемент ТТЛ выполняет логическую операцию И-НЕ, в принципе повторяет структуру ДТЛ микросхем и в то же время за счёт использования многоэмиттерного транзистора, объединяет свойства диода и транзисторного усилителя что позволяет увеличить быстродействие, снизить потребляемую мощность и усовершенствовать технологию изготовления микросхемы. ТТЛ получила широкое распространение в компьютерах, электронных музыкальных инструментах, а также в КИПиА (контрольно-измерительной аппаратуре и автоматике). Благодаря широкому распространению ТТЛ входные и выходные цепи электронного оборудования часто выполняются совместимыми по электрическим характеристикам с ТТЛ. Максимальное напряжение в схемах с ТТЛ может достигать 24В, однако это приводит к большому уровню паразитного сигнала. Достаточно малый уровень паразитного сигнала при сохранении достаточной эффективности достигается при напряжении 5В, поэтому данная цифра и вошла в технический регламент ТТЛ. ТТЛ стала популярной среди разработчиков электронных систем после того, как в 1965 году фирма Texas Instruments представила серию интегральных микросхем 7400. Данная серия микросхем стала промышленным стандартом, но ТТЛ-микросхемы производятся и другими компаниями. Более того, фирма Texas Instruments не была первой, кто начал выпуск ТТЛ микросхем, несколько ранее его начали фирмы Sylvania и Transitron. Тем не менее промышленным стандартом стала именно серия 74 фирмы Texas Instruments, что в значительной мере объясняется большими производственными мощностями фирмы Texas Instruments, а также её усилиями по продвижению серии 74. Поскольку биполярные интегральные ИМС серии 74 фирмы Texas Instruments стали наиболее распространёнными, их функционально и параметрически повторяет продукция других фирм (Advanced Micro Devices, серия 90/9N/9L/9H/9S Fairchild, Harris, Intel, Intersil, Motorola, National и т.д). Важность ТТЛ заключается в том, что ТТЛ-микросхемы оказались более пригодны для массового производства и при этом превосходили по параметрам ранее выпускавшиеся серии микросхем (резисторно-транзисторная и диодно-транзисторная логика). Принцип работы
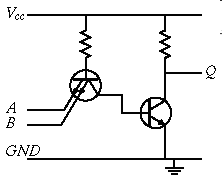
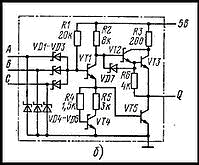
Упрощённая схема элемента 2И-НЕ. Принцип работы ТТЛ с простым инвертором: Биполярные транзисторы могут работать в четырех режимах: отсечки, нормально активный, инверсно активный и насыщения. В инверсно активном режиме эмиттерный переход закрыт, а коллекторный переход открыт. В инверсном режиме коэффициент усиления транзистора значительно меньше, чем в нормальном режиме, из-за несимметричного конструктивного исполнения переходов база-коллектор и база-эмиттер.
При нулевом уровне на любом входе многоэмиттерного транзистора VT1 (на упрощённой схеме — слева) он работает в нормальном режиме и формирует на базе VT2 потенциал близкий к нулю. В этом состоянии неосновные носители из базы VT2 рассасываются не только через коллектор, но и через открытый VT1. Если ноль подаётся на один из входов VT1, то наблюдается максимальный входной ток I=(E-0,7)/R1. В этом случае через другие эмиттерные переходы может наблюдаться паразитный ток. Чтобы он не был слишком велик неиспользуемые входы элемента присоединяются к источнику питания +5В, −5В через резистор с сопротивлением 1кОм, который может работать на 10 входов ТТЛ. Если свободные входы не подключаются ни к чему, то логика работы схемы сохраняется но паразитная ёмкость входных цепей будет уменьшать быстродействие цепи из расчёта 2 нс на 1 вход. Свободные входы могут воспринимать сигнал помехи, который может привести к сбою в работе схемы.
Если на все входы поступает уровень логической единицы, то VT1 окажется инверсно-включенным, ток R1 течёт через коллектор VT1 в базу VT2, на выходе формируется нуль. Если резистор R2 не используется, то мы имеем дело с элементом с открытым коллектором, у которого в условном обозначении используется дополнительный символ.

|
| |
| |
| SlaVe4U | Дата: Среда, 12.01.2011, 02:47 | Сообщение # 9 |
|
Главный Администратор
Группа: Администраторы
Сообщений: 320
Награды: 23
Репутация: 222
Статус: Offline
| Логический элемент 3И-НЕ в серии микросхем 74LS(К555)[1] ТТЛ-логика (как и ТТЛШ) является прямым наследником ДТЛ и использует тот же принцип действия. Входной ТТЛ-транзистор (в отличие от обычного) имеет несколько, обычно от 2 до 8, эмиттеров. Эти эмиттеры выполняют роль входных диодов (если сравнивать с ДТЛ). Многоэмиттерный транзистор по сравнению с применявшейся в схемах ДТЛ сборкой из отдельных диодов занимает меньше места на кристалле и обеспечивает более высокое быстродействие. Следует отметить, что в микросхемах ТТЛШ, начиная с серии 74LS, вместо многэмиттерного транзистора используется сборка диодов Шоттки (серия 74LS) или PNP транзисторы в сочетании с диодами Шоттки (серии 74AS, 74ALS), так что фактически произошёл возврат к ДТЛ. Название ТТЛ заслуженно носят лишь серии 74, 74H, 74L, 74S, содержащие многоэмиттерный транзистор. Все более поздние серии многоэмиттерного транзистора не содержат, фактически являются ДТЛ и носят название ТТЛШ (ТТЛ Шоттки) лишь «по традиции», будучи развитием именно ДТЛ. Транзисторно-транзисторная логика с диодами Шоттки (ТТЛШ) В ТТЛШ используются транзисторы Шоттки, в которых барьер Шоттки не позволяет транзистору войти в режим насыщения в результате чего диффузионная ёмкость мала и задержки переключения малы, а быстродействие высокое. ТТЛШ-логика отличается от ТТЛ наличием диодов Шоттки в цепях база — коллектор, что исключает насыщение транзистора, а также наличием демпфирующих диодов Шоттки на входах (редко на выходах) для подавления импульсных помех, образующихся из-за отражений в длинных линиях связи (длинной считается линия, время распространения сигнала в которой больше длительности его фронта, для самых быстрых ТТЛШ микросхем линия становится длинной начиная с длины в несколько сантиметров).
Серии ТТЛ-микросхем отечественного производства
106 — ранняя серия ТТЛ микросхем, пониженной степени интеграции (не более 2 логических элементов в одном корпусе), предназначенная для тяжёлых условий эксплуатации (военная аппаратура, космос, и т. п.). Не имеет аналогов среди микросхем фирмы Texas Instruments.
133 и 155 соответствуют сериям 54 и 74;
130, 131 — сериям 54H и 74H;
134, КР134 — сериям 54L и 74L;
136 и 158 — близки к сериям 54L и 74L, но имеют вдвое большее энергопотребление при несколько большем быстродействии;
530 и 531 — сериям 54S и 74S;
533 и 555 — сериям 54LS и 74LS;
1530 — серии 74AS (приблизительное соответствие);
1531 — серии 74F;
1533 — серии 74ALS;

|
| |
| |
| SlaVe4U | Дата: Среда, 12.01.2011, 02:48 | Сообщение # 10 |
|
Главный Администратор
Группа: Администраторы
Сообщений: 320
Награды: 23
Репутация: 222
Статус: Offline
| 7.Транзисторно-транзисторная логика. Особенности построения и применения. Основные параметры. Логические элементы с открытым коллектором и тремя состояниями выхода.
Классификация электронных транзисторных физических реализаций логических элементов Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
РТЛ (резисторно-транзисторная логика)
ДТЛ (диодно-транзисторная логика)
ТТЛ (транзисторно-транзисторная логика)
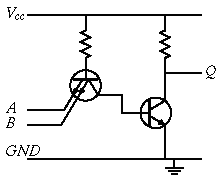
Упрощённая схема двухвходового элемента И-НЕ ТТЛ . Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом. В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами. Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используются в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включенным в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включенным по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
ТТЛШ (то же с диодами Шоттки) Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
КМОП (логика на основе комплементарных ключей на МОП транзисторах)
ЭСЛ (эмиттерно-связанная логика) Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160-200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.

|
| |
| |
| SlaVe4U | Дата: Среда, 12.01.2011, 02:48 | Сообщение # 11 |
|
Главный Администратор
Группа: Администраторы
Сообщений: 320
Награды: 23
Репутация: 222
Статус: Offline
| Инвертор Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
[править]
Применение логических элементов Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.

|
| |
| |
| SlaVe4U | Дата: Среда, 12.01.2011, 02:49 | Сообщение # 12 |
|
Главный Администратор
Группа: Администраторы
Сообщений: 320
Награды: 23
Репутация: 222
Статус: Offline
| 8. Транзисторная логика на комплементарных МОП-структурах. Особенности построения и применения логических элементов.
МОП-транзисторная логика на комплементарных транзисторах (КМОП). Схема строится на комплементарных МОП-транзисторах. В качестве логических используются два транзистора, один из которых с n-каналом, а другой - с р-каналом. Логические ИМС на их основе являются наиболее перспективными. Мощность, потребляемая ими в статическом режиме, составляет десятки нановатт, быстродействие около 10 МГц, они обладают большим логическим перепадом. Однако технология изготовления транзисторов с р- n-каналами на одном кристалле сложна и трудоемка.
Эмиттерно-связанная логика (ЭСЛ). Основу этой группы ИМС составляет переключатель тока, представляющий собой ключевой элемент на транзисторах с объединенным эмиттером. Такие логические ИМС наиболее быстродействующие.
Интегральная инжекционная логика (И2Л). Эта логика не имеет аналогов в дискретном исполнении и является новым направлением, которое способствует миниатюризации цифровых приборов. В основе построения микросхем на И2Л используется базовая структура, состоящая из комплементарной пары биполярных транзисторов. Транзистор p-n-р работает в режиме источника тока (выполняет функции инжектора носителей заряда), а многоэмиттерный транзистор n-p-n работает как инвертор. Поэтому эту логику можно назвать логикой с инжекционным питанием. Один элемент И2Л занимает очень малую площадь, и потребляемая им мощность незначительна. Поэтому множество таких элементов можно объединить в схему с высокой степенью интеграции. МОП-структура
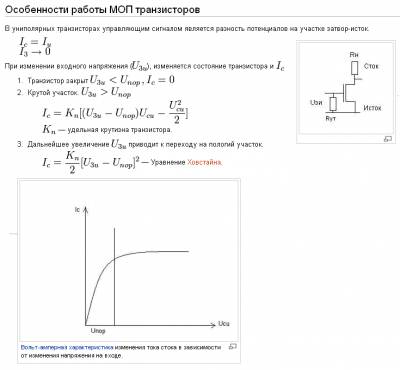
Это версия страницы, ожидающая проверки. Последняя подтверждённая версия датируется 15 января 2010. МОП структура - (МОП - Металл - Оксид - полупроводник) наиболее широко используемый тип полевых транзисторов. Название МОП является традиционным названием такой структуры. Структура состоит из металла и полупроводника, разделённых слоем оксида SiO2. В общем случае структуру называют МДП (металл - диэлектрик - полупроводник). Транзисторы на основе МОП-структур, в отличие от биполярных,управляются напряжением, а не током и называются униполярными транзисторами, так как для его работы необходимо наличие носителей заряда только одного типа. Транзисторы на основе МОП-структур называют полевыми или МОП-транзисторами (в зарубежной литературе MOSFET - metall-oxyde-semiconductor field effect transistor), которые существуют двух типов: n-канальные и p-канальные.

|
| |
| |
| SlaVe4U | Дата: Среда, 12.01.2011, 02:49 | Сообщение # 13 |
|
Главный Администратор
Группа: Администраторы
Сообщений: 320
Награды: 23
Репутация: 222
Статус: Offline
| 9. Схемы сопряжения интегральных микросхем ТТЛ и КМОПТЛ.
Применение ТТЛ микросхем Для успешного применения ИС ТТЛ в электронной вычислительной аппаратуре (ЭВА) и обеспечения надежной работы необходимо знать технические характеристики ИС, строго руководствоваться требованиями технических условий по режимам эксплуатации и правилам электромонтажа, не допускать выхода параметров за значения, указанные для предельных режимов эксплуатации. Только тогда можно избежать ошибок, которые, несмотря на правильное логическое проектирование схемы, не позволяют обеспечить ее надежную работу. В данной главе изложены некоторые особенности применения ИС ТТЛ, которые не всегда учитываются разработчиками ЭВА, что приводит к нарушениям электрических режимов эксплуатации ИС, снижению надежности ИС и аппаратуры в целом. Особенности применения логических элементов ТТЛ Обеспечение нагрузочной способности по постоянному току при работе ИС ТТЛ друг на друга. Все ИС ТТЛ по логическим уровням напряжения совместимы друг с другом. Однако по нагрузочной способности ИС разных серий имеют известные различия. В пределах одной серии ИС, как правило, обладают одинаковой нагрузочной способностью или, иначе, одинаковым коэффициентом разветвления, определяемым числом входов эквивалентных ЛЭ, которые могут быть подключены к выходу каждого из них. Исключение составляют микросхемы, содержащие логические элементы с более мощными выходными каскадами, например буферные формирователи, схемы сопряжения с магистралью, схемы с повышенным коэффициентом разветвления. Чем выше нагрузочная способность логических элементов ИС, тем больше их логические возможности. Превышение нагрузочной способности по отношению к заданной техническими условиями приводит к ухудшению других параметров ИС: снижению быстродействия, увеличению потребляемой мощности, ухудшению помехоустойчивости и надежности. Поэтому при конструировании ЭВА необходимо правильно оценивать нагрузочную способность микросхемы по постоянному току, особенно при работе микросхем разных серий друг на друга, и стремиться к снижению нагрузки. При работе ИС друг на друга выходной ток ЛЭ определяется входными токами управляемых ИС и задается для неблагоприятного рабочего режима в допустимых пределах изменения температуры окружающей среды и напряжения питания для входного напряжения как низкого (лог. 0), так и высокого (лог. 1) уровня. При наличии на одном из входов логического элемента ИС (например, серии К155) напряжения, соответствующего лог. 0, через эмиттер входного транзистора вытекает максимальный ток. Для базового логического элемента (со стандартным выходом) ИС серии К155 он составляет 1,6 мА и имеет отрицательный знак. При поступлении на каждый вход сигнала, равного единице, через эмиттер входного транзистора втекает ток 40 мкА. При этом токи, втекающие в микросхему, имеют положительный знак.

|
| |
| |
| SlaVe4U | Дата: Среда, 12.01.2011, 02:50 | Сообщение # 14 |
|
Главный Администратор
Группа: Администраторы
Сообщений: 320
Награды: 23
Репутация: 222
Статус: Offline
| 10. Триггеры нетактируемые и тактируемые. Примеры построения. Отличительные признаки.
Триггеры реклама в интернет Страница: 1/3 1. Общие сведения Устройство, имеющее два устойчивых состояния, называют триггером. Он имеет два выхода, один из них называют прямым, а другой — инверсным. Потенциалы на них взаимно инвертированы: лог. 1 на одном выходе соответствует лог. 0 на другом. С приходом переключающих (запускающих) сигналов переход триггера из одного состояния в другое происходит лавинообразно, и потенциалы на выходах меняются на противоположные. В интервале между переключающими сигналами состояние триггера не меняется, т. е. триггер "запоминает" поступление сигналов, отражая это величиной потенциала на выходе. Это дает возможность использовать его как элемент памяти. При лавинообразных переключениях на выходе триггера формируются прямоугольные импульсы с крутыми фронтами. Это позволяет использовать триггер для формирования прямоугольных импульсов из напряжения другой формы (например, из синусоидального). При двух последовательных переключениях триггера на выходе формируется один импульс, т.е. триггер можно использовать как делитель частоты переключающих сигналов с коэффициентом, равным двум. Триггеры можно разделить на не тактируемые и тактируемые. Не тактируемый (асинхронный) триггер может менять свое состояние
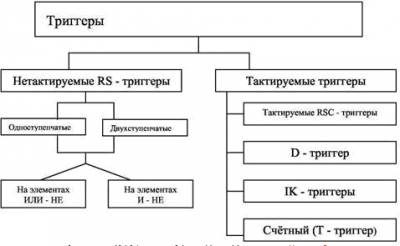
Рис.1 переключающими сигналами в любое время. Тактируемый (синхронный) триггер переключается синхронно с поступлением специального тактирующего импульса. Эти и другие типы триггеров, показанные в таблице классификации, подробно рассмотрены далее. Промышленность выпускает разнообразные типы триггеров в интегральном исполнении. Кроме того, они могут быть выполнены на цифровых интегральных микросхемах, операционных усилителях и на транзисторах. Рис.1. 2. Не тактируемые триггеры На выходе элемента И-НЕ (ИЛИ-НЕ) имеется инвертор (усилитель). В структуре из двух таких элементов можно обеспечить положительную обратную связь, если вход одного элемента соединить с выходом другого, и баланс амплитуд. Такой структурой является RS-триггер. Он имеет два выхода: прямой () и инверсный () и два входа: S — установки прямого выхода в 1 (говорят: "установки триггера в 1") и R — установки триггера в 0. Такой триггер является асинхронным RS-триггером. Он применяется самостоятельно, а также в качестве запоминающей ячейки входит в состав более сложных интегральных триггеров.

|
| |
| |
| SlaVe4U | Дата: Среда, 12.01.2011, 02:52 | Сообщение # 15 |
|
Главный Администратор
Группа: Администраторы
Сообщений: 320
Награды: 23
Репутация: 222
Статус: Offline
| 11. Нетактируемый и тактируемый потенциалом RS-триггеры.
2.1. Структуры триггеров
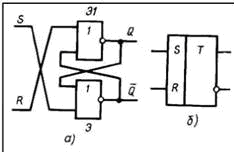
RS-триггер на элементах ИЛИ-НЕ (рис. 2,а). Прежде всего рассмотрим воздействие на такой триггер комбинаций сигналов S=1, R=1 и S=0, R=0. Сочетание S=1, R=1 является запрещенным, так как при нем на обоих выходах триггера устанавливаются логические 0 и после снятия входных сигналов состояние его непредсказуемо. Для элемента ИЛИ-НЕ логический 0 является пассивным сигналом: с его поступлением на вход состояние выхода элемента не изменяется. Поэтому появление комбинации S=0, R=0 не изменяет состояния триггера. Логическая 1 для элемента ИЛИ-НЕ является активным сигналом: наличие ее на входе элемента однозначно определяет на его выходе логический 0 вне зависимости от сигнала на другом входе. Отсюда следует, что переключающим сигналом для рассматриваемого триггера является логическая 1, а также то, что вход S (установки триггера в состояние Q=1) должен быть связан с элементом, выход которого принят за . Из сказанного ясно, что для переключения триггера в состояние Q=1 на его входы следует подать комбинацию S=1, R=0, а для переключения в состояние Q=0 — комбинацию S=0,R=1. Пусть триггер (рис. 2,а) находится в состоянии 0 (Q=0, =1), а на входах действуют сигналы S=0, R=0. Для его переключения в состояние Q=1 подадим на входы комбинацию о S=1, R=0. Тогда на выходе элемента Э2 установится логический 0, на входах элемента Э1 будут одновременно присутствовать, логические 0, и на выходе Q установится логическая 1 — триггер переключается в новое состояние (Q=1, =0). Для его переключения из этого состояния на входы должна поступить комбинация S=0, R=1. После этого на выходе Q будет логический 0, на входах элемента Э2 одновременно окажутся логические 0 и его выход примет потенциал, соответствующий =1, —триггер переключается в состояние Q=0, =1.
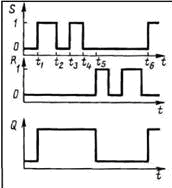
Рис.3. Из изложенного следует, что время переключения триггера (tпер) равно удвоенному времени переключения логического элемента (удвоенному времени задержки — 2tз). Часто, предусматривая запас, принимают tпер=3tз. Для надежного переключения триггера длительность входного переключающего сигнала не должна быть меньше tпер. Условное изображение RS-триггера приведено на рис. 2,б. На рис.3 приведена идеализированная временная диаграмма RS-триггера, на которой время переключения триггера принято равным нулю. Предполагается, что до момента t1 S=0, R=0, а триггер находится в состоянии Q=0. В момент t1 комбинация S=1, R=0 переключает триггер в состояние Q=1. При t=t2 на входах устанавливается сочетание S=0, R=0, при котором состояние триггера сохраняется прежним. Комбинация S=1, R=0, появляющаяся в момент t3, и комбинация S=0, R=0 в момент t4 никаких изменений не вносят, по-прежнему Q=1. Только в момент t5 сочетание S=0, R=1 вызывает переключение триггера в состояние Q=0. Вслед за этим изменение логической переменной на входе R состояния триггера не меняет. Новое переключение происходит в момент t6 при поступлении на входы комбинации S=1, R=0. Заметим, что запрещенное сочетание сигналов S=1, R=1 на диаграмме отсутствует.
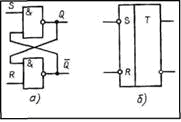
RS -триггер на элементах И-НЕ (рис. 4,а). Для элемента И-НЕ активным сигналом является логический 0: наличие его хотя бы на одном входе обусловливает на выходе логическую 1 независимо от сигналов на других входах. Логическая 1 для такого элемента является пассивным сигналом: с ее поступлением на вход состояние выхода элемента не изменяется. В силу сказанного триггер на элементах И-НЕ переключается логическим 0. На условном изображении такого триггера (рис. 4,б) это отражают инверсными входами.

|
| |
| |
|